Contoh
. Peta Karnaugh digunakan untuk memfasilitasi penyederhanaan aljabar Boolean fungsi. . Berikut ini adalah fungsi Aljabar Boolean unsimplified dengan variabel Boolean A, B, C, D, dan invers mereka. : Mereka dapat direpresentasikan dalam dua notasi yang berbeda:- . f (A, B, C, D) = Σ (6,8,9,10,11,12,13,14) Catatan: Nilai-nilai di dalam Σ adalah minterm untuk memetakan (baris yaitu yang memiliki output 1 dalam kebenaran tabel).
| # # | A Sebuah | B B | C C | D D | f ( A , B , C , D ) f (A, B, C, D) |
|---|---|---|---|---|---|
| 0 0 | 0 0 | 0 0 | 0 0 | 0 0 | 0 0 |
| 1 1 | 0 0 | 0 0 | 0 0 | 1 1 | 0 0 |
| 2 2 | 0 0 | 0 0 | 1 1 | 0 0 | 0 0 |
| 3 3 | 0 0 | 0 0 | 1 1 | 1 1 | 0 0 |
| 4 4 | 0 0 | 1 1 | 0 0 | 0 0 | 0 0 |
| 5 5 | 0 0 | 1 1 | 0 0 | 1 1 | 0 0 |
| 6 6 | 0 0 | 1 1 | 1 1 | 0 0 | 1 1 |
| 7 7 | 0 0 | 1 1 | 1 1 | 1 1 | 0 0 |
| 8 8 | 1 1 | 0 0 | 0 0 | 0 0 | 1 1 |
| 9 9 | 1 1 | 0 0 | 0 0 | 1 1 | 1 1 |
| 10 10 | 1 1 | 0 0 | 1 1 | 0 0 | 1 1 |
| 11 11 | 1 1 | 0 0 | 1 1 | 1 1 | 1 1 |
| 12 12 | 1 1 | 1 1 | 0 0 | 0 0 | 1 1 |
| 13 13 | 1 1 | 1 1 | 0 0 | 1 1 | 1 1 |
| 14 14 | 1 1 | 1 1 | 1 1 | 0 0 | 1 1 |
| 15 15 | 1 1 | 1 1 | 1 1 | 1 1 | 0 0 |
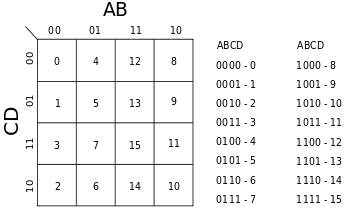
[ edit ] Karnaugh map [ sunting ] peta Karnaugh
. Variabel input dapat dikombinasikan dalam 16 cara yang berbeda, sehingga peta Karnaugh memiliki 16 posisi, dan karena itu diatur dalam 4 × 4 grid.. Angka biner dalam peta merupakan keluaran fungsi untuk setiap kombinasi input tertentu.. Jadi 0 adalah ditulis di sudut paling kiri atas dari peta karena ƒ = 0 bila A = 0, B = 0, C = 0, D = 0. . Demikian pula kita tandai sudut kanan bawah sebagai 1 karena A = 1, B = 0, C = 1, D = 0 memberikan ƒ = 1. Perhatikan bahwa nilai-nilai yang diperintahkan dalam kode Gray , sehingga tepat satu variabel perubahan antara sepasang sel yang berdekatan.
. Setelah peta Karnaugh telah dibangun tugas berikutnya adalah untuk menemukan istilah minimal untuk digunakan dalam ekspresi akhir. . Istilah-istilah ini ditemukan oleh kelompok mengelilingi 1s dalam peta. . Kelompok-kelompok harus persegi panjang dan harus memiliki luas yang merupakan kekuatan dua (yaitu 1, 2, 4, 8 ...). . Persegi panjang harus seluas mungkin tanpa mengandung 0s apapun. s. Pengelompokan optimal dalam peta ini ditandai oleh, garis hijau merah dan biru. . Perhatikan bahwa kelompok mungkin tumpang tindih. In this example, the red and green groups overlap. Dalam contoh ini, kelompok merah dan hijau tumpang tindih. T. Kelompok merah adalah persegi 2 × 2, kelompok hijau adalah 4 × 1 persegi panjang, dan daerah tumpang tindih ditunjukkan dalam coklat.
toroidally terhubung, yang berarti bahwa kelompok-kelompok persegi panjang bisa membungkus di sekitar tepi, sehingga
 adalah istilah yang valid, meskipun bukan bagian dari minimal set-ini mencakup Minterms 8, 10, 12, dan 14.
adalah istilah yang valid, meskipun bukan bagian dari minimal set-ini mencakup Minterms 8, 10, 12, dan 14. Mungkin istilah yang paling sulit-untuk-memvisualisasikan wrap-sekitar adalah
 . yang meliputi empat sudut-ini mencakup minterm 0, 2, 8, 10.
. yang meliputi empat sudut-ini mencakup minterm 0, 2, 8, 10. [ edit ] Solution [ sunting ] Solusi
For the Red grouping: Untuk pengelompokan Merah:
- . Variabel Sebuah mempertahankan keadaan yang sama (1) di seluruh keliling, oleh karena itu harus dimasukkan dalam jangka untuk mengelilingi merah.
- Variabel B tidak mempertahankan negara yang sama (itu bergeser dari 1 ke 0), dan karenanya harus dikeluarkan.
- , Karena C adalah 0, itu harus dinegasikan sebelum dimasukkan (dengan demikian,
 ). ).
). ). - . Perubahan D, sehingga dikecualikan juga.

Untuk pengelompokan Hijau kita melihat bahwa A, B mempertahankan negara yang sama, tetapi C dan D berubah. B adalah 0 dan harus menegasikan sebelum dapat disertakan. is Jadi istilah kedua adalah

I Dengan cara yang sama, pengelompokan Biru memberikan istilah

Solusi dari setiap pengelompokan digabungkan menjadi:
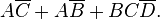
: Tiga istilah untuk menutupi terbalik semua ditampilkan dengan kotak abu-abu dengan batas-batas warna yang berbeda:
- brown— coklat-
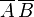
- gold— emas-

- blue— B C D biru B C D



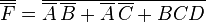


0 komentar:
Posting Komentar